零階保持（zero-order hold）簡稱ZOH，是傳統數位模擬轉換器（DAC）上信號重建的數學模型。此作法會在各取樣區間之間，讓信號維持之前的值，以此方式將離散信號轉換為連續信號，在電子通訊上有許多的應用。

時域模型

　　.

　　零階保持可以從取樣數列x[n]重建為以下的連續時間信號，假設每一個取樣的時間間隔都是T：

　　{\displaystyle x_{\mathrm{ZOH}}(t)\=\sum _{n=-\infty}^{\infty}x[n]\cdot\mathrm{rect}\left({\frac{t-T/2-nT}{T}}\right)\,}{\displaystyle x_{\mathrm{ZOH}}(t)\=\sum _{n=-\infty}^{\infty}x[n]\cdot\mathrm{rect}\left({\frac{t-T/2-nT}{T}}\right)\,}

　　其中{\displaystyle\mathrm{rect}(),}{\displaystyle\mathrm{rect}(),}為矩形函數。

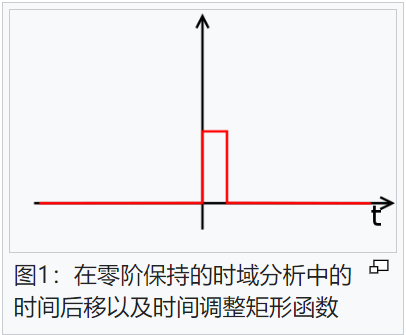
　　函數{\displaystyle\mathrm{rect}\left({\frac{t-T/2}{T}}\right)}{\displaystyle\mathrm{rect}\left({\frac{t-T/2}{T}}\right)}如圖1所示，而{\displaystyle x_{\mathrm{ZOH}}(t)\,}{\displaystyle x_{\mathrm{ZOH}}(t)\,}是分段常數函數，如圖2所示。

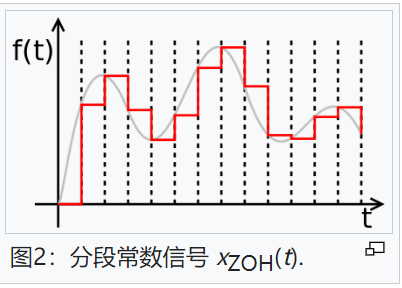
頻域模型

　　上述ZOH輸出的方程式也可以表示為沖激響應分段常數函數（rect函數）的線性時不變濾波器之輸出，輸入則是狄拉克δ函數乘以取樣數值所產生的脈沖序列。濾波器可以在頻域下進行分析，和其他的信號重建方式進行比較，例如依采樣定理建議的惠特克-香農插值公式，或是在二個取樣點之間線性內插的一階保持。

　　在此作法中，會將狄拉克δ函數的脈沖序列xs(t)經過低通濾波器還原為連續信號x(t)。

　　雖然實際的數位類比轉換器（DAC）不是以此方式進行，不過其其特性可以建模為將假想脈沖序列xs(t)用LTI濾波后所得的特性，而此濾波器的特性是每一個輸入脈沖都可以產生持續到下一個取樣點的常數步階輸出。

　　一開始先從取樣訊號，配合delta函數建立連續訊號：

　　{\displaystyle{\begin{aligned}x_{s}(t)&=\sum _{n=-\infty}^{\infty}x[n]\cdot\delta\left({\frac{t-nT}{T}}\right)\\&{}=T\sum _{n=-\infty}^{\infty}x[n]\cdot\delta(t-nT).\end{aligned}}}{\displaystyle{\begin{aligned}x_{s}(t)&=\sum _{n=-\infty}^{\infty}x[n]\cdot\delta\left({\frac{t-nT}{T}}\right)\\&{}=T\sum _{n=-\infty}^{\infty}x[n]\cdot\delta(t-nT).\end{aligned}}}

　　其中T的比例是因為將delta函數配合時間調整比例而產生的，其意思是使xs(t)的平均值等于在取樣的數值，因此低通濾波器的直流增益設定為1即可。有些文獻使用這種比例調整方式，不過許多文獻不考慮delta函數的系數'T，因此低通濾波器會有一個直流增益T，也就會隨取樣時間而變化。

　　零階保持是假想的濾波器或線性系統，可以將調變后的迪拉克脈沖xs(t)轉換為片段連續的訊號（如圖2）。

　　{\displaystyle x_{\mathrm{ZOH}}(t)\,=\sum _{n=-\infty}^{\infty}x[n]\cdot\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{1}{2}}\right)\}{\displaystyle x_{\mathrm{ZOH}}(t)\,=\sum _{n=-\infty}^{\infty}x[n]\cdot\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{1}{2}}\right)\}

　　其等效的沖激響應（如圖4）為：

　　{\displaystyle h_{\mathrm{ZOH}}(t)\,={\frac{1}{T}}\mathrm{rect}\left({\frac{t}{T}}-{\frac{1}{2}}\right)={\begin{cases}{\frac{1}{T}}&{\mbox{if}}0\leq t<T\\0&{\mbox{otherwise}}\end{cases}}\}{\displaystyle h_{\mathrm{ZOH}}(t)\,={\frac{1}{T}}\mathrm{rect}\left({\frac{t}{T}}-{\frac{1}{2}}\right)={\begin{cases}{\frac{1}{T}}&{\mbox{if}}0\leq t<T\\0&{\mbox{otherwise}}\end{cases}}\}

　　其等效頻率響應為沖激響應的傅里葉變換。

　　{\displaystyle H_{\mathrm{ZOH}}(f)\,={\mathcal{F}}\{h_{\mathrm{ZOH}}(t)\}\,={\frac{1-e^{-i2\pi fT}}{i2\pi fT}}=e^{-i\pi fT}\mathrm{sinc}(fT)\}{\displaystyle H_{\mathrm{ZOH}}(f)\,={\mathcal{F}}\{h_{\mathrm{ZOH}}(t)\}\,={\frac{1-e^{-i2\pi fT}}{i2\pi fT}}=e^{-i\pi fT}\mathrm{sinc}(fT)\}

　　其中{\displaystyle\mathrm{sinc}(x)\}{\displaystyle\mathrm{sinc}(x)\}是正規化的Sinc函數{\displaystyle{\frac{\sin(\pi x)}{\pi x}}}{\displaystyle{\frac{\sin(\pi x)}{\pi x}}}，常用在數位信號處理中。

　　ZOH的傳遞函數拉普拉斯變換可以用將s替代為i 2πf而得

　　{\displaystyle H_{\mathrm{ZOH}}(s)\,={\mathcal{L}}\{h_{\mathrm{ZOH}}(t)\}\,={\frac{1-e^{-sT}}{sT}}\}{\displaystyle H_{\mathrm{ZOH}}(s)\,={\mathcal{L}}\{h_{\mathrm{ZOH}}(t)\}\,={\frac{1-e^{-sT}}{sT}}\}

　　實際的數位類比轉換器（DAC）不會輸出狄拉克δ函數的序列xs(t)（因此，若是理想的低通濾波，會在取樣前得到獨特的帶寬受限制的訊號），會輸出方波的序列xZOH(t)（階躍函數），因此ZOH在DAC的頻率響應中會有一個本質造成的影響，在頻率較高時，會有輕微的信號衰減（在奈奎斯特頻率處降低3.9224 dB，對應sinc(1/2)=2/π）。此衰減是因為傳統DAC的“保持”特性，不是因為在傳統類比數位轉換器前面的取樣保持電路的影響。

關于零階保持，小編為大家就分享這些。歡迎聯系我們合運電氣有限公司，以獲取更多相關知識。